Sorting algorithms are fundamental to our every day life, so much so that I think most people don’t even recognise just how important they truly are. They’re so ingrained in most software we use that we never really need to think about how these algorithms actually work. Even from a programming standpoint, sorting functions are prebuilt and come as standard functions.
There are many sorting algorithms (see here) that we could choose from. A visual demonstration of how some sorting algorithms work can be see here:
Generally speaking we want algorithms to scale by 
, where 
is the size of the original list. Unfortunately no sorting algorithm performs this fast — in fact the best performing sorting algorithms usually scale by 
(for context a poorly performing sorting algorithm, like bubble sort, scales by 
).
One of the most popular sorting algorithms is merge sort, which works in the following way:
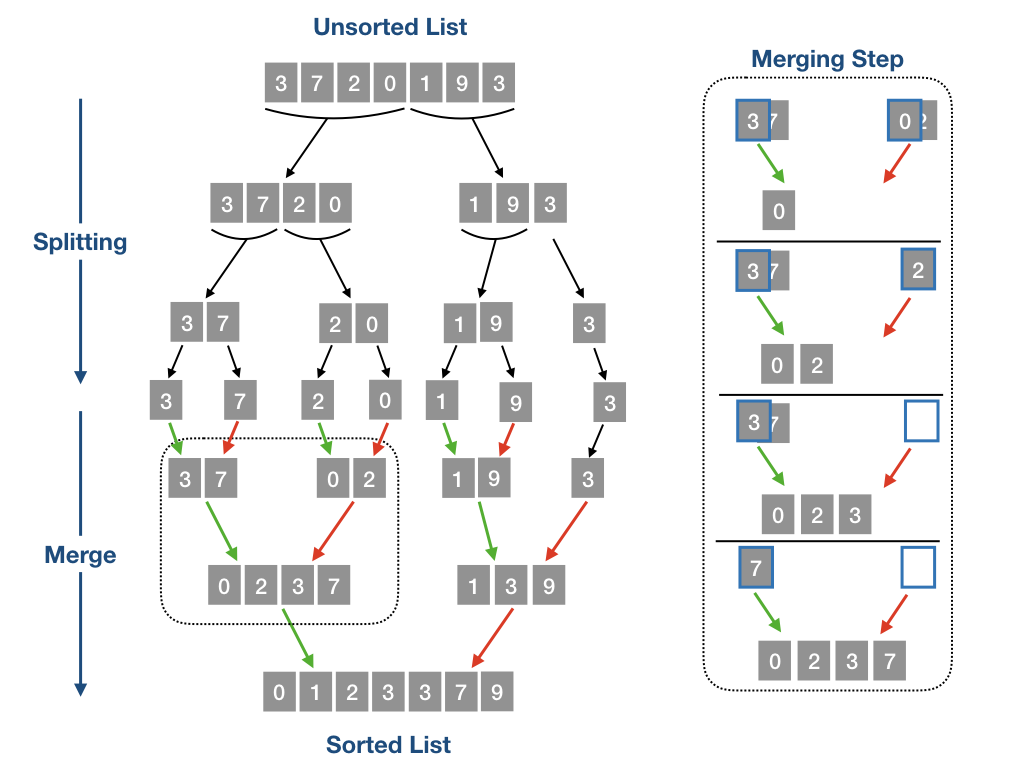
Merge sort works by successively merging two sorted list. The merging step is shown in the diagram above. The first elements of the two list are compared. The smallest is added to the merged set and this continues until the two lists are fully merge. The C++ code to do this is written as:
void _merge(float arr1[], int size1, float arr2[],
int size2, float arrm[]){
// This function takes 5 arguments:
// arr1 : the 1st sorted list.
// size1 : the number of elements in arr1.
// arr2 : the 2nd sorted list.
// size2 : the number of elements in arr2.
// arrm : the merged sorted list.
int i=0, j=0, k=0; // integers used to account for
// where we are in each list. first check that k,
// which iterates through the merged list, is not
// larger than the combined length of the two lists.
while(k < size1+size2){
// check that both i and j which respectively
// count through arr1 and arr2 are not larger
// than the number of elements in those two lists.
if(i<size1 && j<size2){
// compares element i of arr1 to element j of
// arr2 and adds the smallest to the merged list.
if(arr1[i] <= arr2[j]){
arrm[k] = arr1[i];
i++;
k++;
}
else{
arrm[k] = arr2[j];
j++;
k++;
}
}
// if all elements of arr2 have already been added
// to the merge list then this will just add the
// remaining elements of arr1.
if(i<size1 && j==size2){
arrm[k] = arr1[i];
i++;
k++;
}
// likewise but for arr1.
if(j<size2 && i==size1){
arrm[k] = arr2[j];
j++;
k++;
}
}
}This is the critical function for merge sort and underpins the core idea behind the algorithm. Unfortunately it relies on the two input list to be pre-sorted. So how do we sort the initial list? Well, there’s a very simple solution to this and that is to split the original list into list that are only a single element long. By definition a list with one item is a sorted list! From here on out we just need to propagate this method to larger and larger portions of the full list.
To manage how many elements need to be compared in each step I created a function called _get_split_count which takes as an input the current merging step that is about to take place (I call this the run):
int _get_split_count(int run){
int split_count;
split_count = pow(2, run-1);
return split_count;
}This simply returns 
. Now that we have this function set up we can move on to the full merge_sort function which looks like this:
void merge_sort(float array[], int size){
// Takes as input:
// array : unsorted list.
// size : length of the list.
int run, split_count, range1, range2, range_mid;
// run : equal to the current merging step.
// split_count : the number of elements considered
// for each sorted list being combined.
// range1 : the first element of the first sorted list.
// range_mid : the first element of the second sorted list.
// range2-1 : the last element of the second sorted list.
run = 1;
split_count = 1;
// this checks that there are at least two lists being compared.
while(((float)size)/((float)split_count) > 2.){
split_count = _get_split_count(run);
for(int i = 0; i < size/(2*split_count) + 1; i++){
range1 = 2*split_count*i;
range2 = 2*split_count*(i+1);
range_mid = 2*split_count*i + split_count;
// checks that range2 is not greater than the
// length of the list.
if(range2 > size){
range2 = size;
}
// checks that range_mid is not greater than the
// length of the list.
if(range_mid > size){
range_mid = size;
}
// if range_mid and range2 are equal than array1
// will already be sorted and array2 is empty.
// No merging is required.
if(range_mid != range2){
// creates three temporary arrays.
float array1[range_mid-range1], array2[range2-range_mid]
float arraym[range2-range1];
// copies over two regions of the list to be compared.
for(int j = 0; j < range_mid-range1; j++){
array1[j] = array[range1 + j];
}
for(int j = 0; j < range2-range_mid; j++){
array2[j] = array[range_mid + j];
}
// merges array1 and array2.
_merge(array1, range_mid-range1, array2,
range2-range_mid, arraym);
// writes over the unsorted part of the array
// with the newly sorted section.
for(int j = 0; j < range2-range1; j++){
array[range1 + j] = arraym[j];
}
}
}
run++;
}
}You can download an example of this code here. The file merge_sort.cpp contains the merge sort code as well as some utility code for printing and creating random arrays. To compile you need to just type g++ -o merge_sort merge_sort.cpp into a terminal and then run ./merge_sort and you should see something like this:
Size of array : 20
Generating randoms...
Printing...
0.346806, 0.761769, 0.0448579, 0.926172, 0.173874, 0.296822, 0.694789,
0.310391, 0.740295, 0.140472, 0.91213, 0.17352, 0.354268, 0.183789,
0.944854, 0.153776, 0.509872, 0.420911, 0.243473, 0.0536147
Merge sort...
Printing sorted randoms...
0.0448579, 0.0536147, 0.140472, 0.153776, 0.17352, 0.173874, 0.183789,
0.243473, 0.296822, 0.310391, 0.346806, 0.354268, 0.420911, 0.509872,
0.694789, 0.740295, 0.761769, 0.91213, 0.926172, 0.944854And that’s how it works. If you have any suggestions to improve the code or the explanation please let me know.